- représentations : binaire, octal, hexadécimal
- calcul booléen
Représentation binaire
Habituellement, nous représentons les valeurs entières dans le système décimal, on dit aussi en base 10. Nous utilisons les dix chiffres de 0 à 9. La position des chiffres définit la valeur associée à ce chiffre. Par exemple, 542 est compris comme
Les différents chiffres correspondent aux puissances successives de 10 :
L'information numérique, qu'il s'agisse de valeurs entières, de textes, d'images, ou de sons est en fin de compte représentée par des suites de 0 et de 1. On parle de bit : un bit peut prendre deux valeurs, 0 ou 1.
Le système binaire permet d'écrire les valeurs entières en n'utilisant que ces les deux chiffres 0 et 1. On utilise alors la base 2.
De même que pour la base 10, les positions des chiffres sont associées aux puissances successives de 2
Ainsi la valeur entière qui correspond à la représentation binaire 101010 est
= 1 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 1 × 2 + 0 × 1
= 42
Il nous faut pouvoir indiquer que 101010 est une représentation binaire et non une représentation décimale, qui serait comprise cent un mille dix (ou encore une représentation dans une autre base...).
On notera par exemple 0b101010 ou 1010102, ou encore 101010.
On distingue donc les valeurs entières (les entiers) et leur représentation.
- On utilise habituellement la représentation décimale.
- D'autres représentations sont possibles. En particulier, dans le monde du numérique, la représentation binaire est souvent utilisée.
À une valeur entière donnée est associée une représentation décimale, mais aussi une représentation binaire.
Donnez les valeurs entières représentées par 0b0100, 0b10101, 0b101, 0b0101 et 0b00101.
Conversion d'un nombre décimal en nombre binaire
Pour expliquer ce type de conversion, on peut revenir sur le système décimal.
Si nous divisons le nombre (543)10 par 10,
nous obtenons comme quotient 54 et 3 comme reste. Cela signifie que ce nombre équivaut à :
(54 x 10) + 3
Le reste 3 est le chiffre
indiquant le nombre d'unités.
En redivisant ce quotient (54) par 10, nous obtenons 5 comme deuxième quotient et 4 comme reste.
Ce reste donne le deuxième chiffre du nombre, donc celui des dizaines.
Enfin, si l'on divise ce deuxième quotient par 10,
nous obtenons 0 et il restera 5 qui représentera le chiffre des centaines.
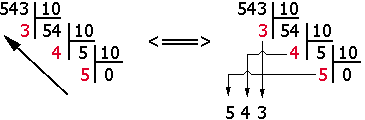
Résumer du principe de conversion
En divisant successivement un nombre par la base (10) et en ne conservant que les restes, on a réussi à exprimer le nombre par des chiffres inférieurs de 10. Mais attention, il faut lire les restes de bas en haut.
Conversion binaire
Maintenant si nous divisons un nombre décimal par 2, le quotient indique le nombre de fois que 2 est contenu dans ce nombre et
le reste indique le chiffre des unités dans l'expression du nombre binaire.
Soit N le nombre, Q1 le quotient et R1 le reste,
nous avons :
N = (Q1 x 2) + (R1 x 1)
N = (Q1 x 21) + (R1 x 20)
Exemple :
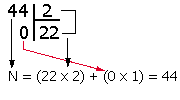
soit :
N = (22 x 2) + (0 x 1) = 44.
Pour obtenir l'expression binaire d'un nombre exprimé en décimal, il suffit de diviser successivement ce nombre par 2 jusqu'à ce que le
quotient obtenu soit égal à 0.
Comme pour la conversion dans le système décimal les restes de ces
divisions lus de bas en haut représentent le nombre binaire.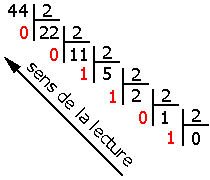
(44)10 = (101100)2.
Octets
octets, poid fort faible.Qu'est ce qu'un octet ? Un bit de poids fort, un bit de poid faible ?
Comment peut -on reconnaître un nombre pair ? un nombre impair ?
Que doit t-on faire pour multiplier un nombre par 2 en binaire ?
Représentation hexadécimale
Relation entre les nombres binaires et les nombres hexadécimaux
Ilfaut exprimer chaque caractère hexadécimal à l'aide de 4 informations binaires.
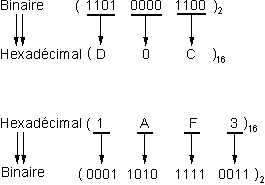
Convertir les nombres suivant dans les trois bases : binaire, décimale et hexadécimale : 18A93 ; 2012 ; 1001100 ; 10523 ; A1D10 ; 1110010011
Utilisation de la calculatrice Windows
Vérifier les résultats obtenus à la manipulation précédente à l'aide de la calculatrice WIndows réglée en mode "Programmeur"







